Writing stylized dotted comic shader in Godot

0 stars

While playing around with Godot engine and shader programming I’ve developed some interestingly looking comic shader with ink-ish look. On this example I want to show you how to implement simple pop style dotted shaders.

It is recommended to read @dreadlocksdude’s shader tutorial first: VFX shader series, lesson 1

Overall, this is an extremely important guide on understanding shader functions as building blocks. We will be heavily using such techniques in this guide.

The idea

While watching the recent Posy video about dot matrix printing, I’ve decided to implement a shader that contained blending CMYK dots in the screen space, such that the image is perpendicular towards the camera (unlike the textures).

In order to avoid unwanted rippling effects during the movement I’ve decided not to overlap the coloured dots, but split them into zones:

So, we will pick the zones, determine the corresponding color, perform some preprocessing effects and render the dots.

As for the test mesh, I will be using the metaball spider model, as this shader looks best on organic surfaces.

Dots function

In order to create the shader, we need to develop the dots function first that returns the color based on position, zone color, background color and rotation of the field.

Firstly, we need to get the formula for the dot in order to determine if we need to return the background color or the color of the dot. This is a simple formula for the ellipse with the origin at \((x_0, y_0)\)

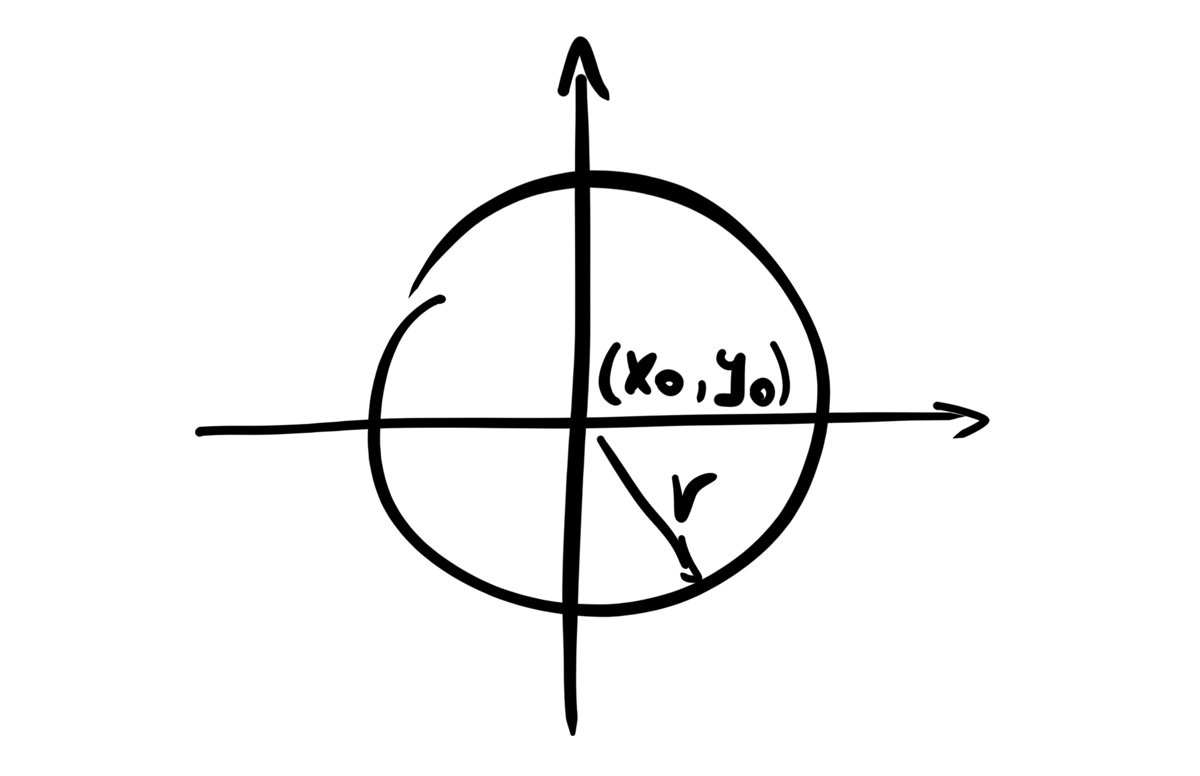
vec3 dots(vec2 pos, vec3 dotcol, vec3 black, float a)
{
    if (pow(pos.x - dot_size, 2) + pow(pos.y - dot_size, 2) <= dot_size*dot_size)
    {
        return dotcol;
    }
    return black;
}

This gives us the single dot at \((x_0, y_0)\), so we need to repeat the function along x and y axis to obtain the matrix of dots. The simpliest way to achieve this is by taking modulo from \(x\) and \(y\). mod(x, n) returns (0, 1, 2, ..., n-1, 0, 1, 2, ...): if we pass the result of this function in the ellipse formula, we obtain the repetition of this ellipse with spacing n anywhere along the space. In the context of shaders, mod function takes floating point numbers aswell.

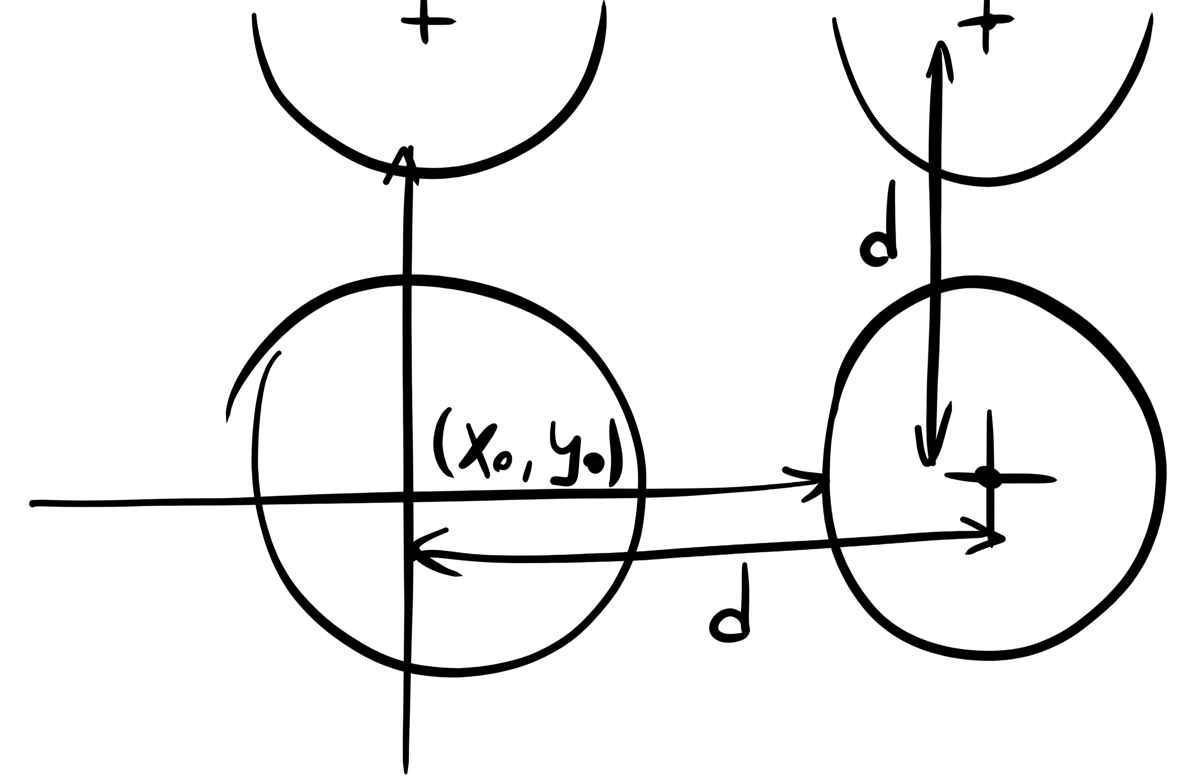
vec3 dots(vec2 pos, vec3 dotcol, vec3 black, float a)
{
    if (pow(mod(pos.x, dot_spacing) - dot_size, 2) + pow(mod(pos.y, dot_spacing) - dot_size, 2) <= dot_size*dot_size)
    {
        return dotcol;
    }
    return black;
}

The last point is the rotation of the dots. We want to rotate the whole space over the point \((0, 0)\), so we need to apply the transformation matrix to the position vector \((x, y)^T\). Note that angle \(a\) must be in radians.

So we nonlinearly transform our position by some matrix and obtain new coordinates that we pass to our code as is.

vec3 dots(vec2 pos, vec3 dotcol, vec3 black, float a)
{
    pos = mat2(vec2(cos(a), sin(a)), vec2(-sin(a), cos(a))) * pos;
    
    if (pow(mod(pos.x, dot_spacing) - dot_size, 2) + pow(mod(pos.y, dot_spacing) - dot_size, 2) <= dot_size*dot_size)
    {
        return dotcol;
    }
    return black;
}

Fragment shader

Firstly, we need to define some uniform variables that can be tuned for each model.

shader_type spatial;

render_mode unshaded;

uniform float power = 3;  // thickness of edge

uniform float dot_spacing = 10;
uniform float dot_size = 2;
uniform float angle = 45;
// ...

It is important to define render_mode unshaded in order to override the color by disabling engine lighting and shading.

// ...
void fragment()
{
    // ...
    ALBEDO = col;
}

So, we need to write fragment function that takes various parameters (vertex position, face normal, …) and sets the albedo (color) of the current fragment (sub-pixel).

Writing a simple shader

After some theory we are finally going to write a simple dot shader. Our fragment function needs to find the edges of the model in order to paint the front facing parts of the model black. We may calculate the cosine of the angle between the camera and normal vector. In other words, we need the dot product between these vectors.

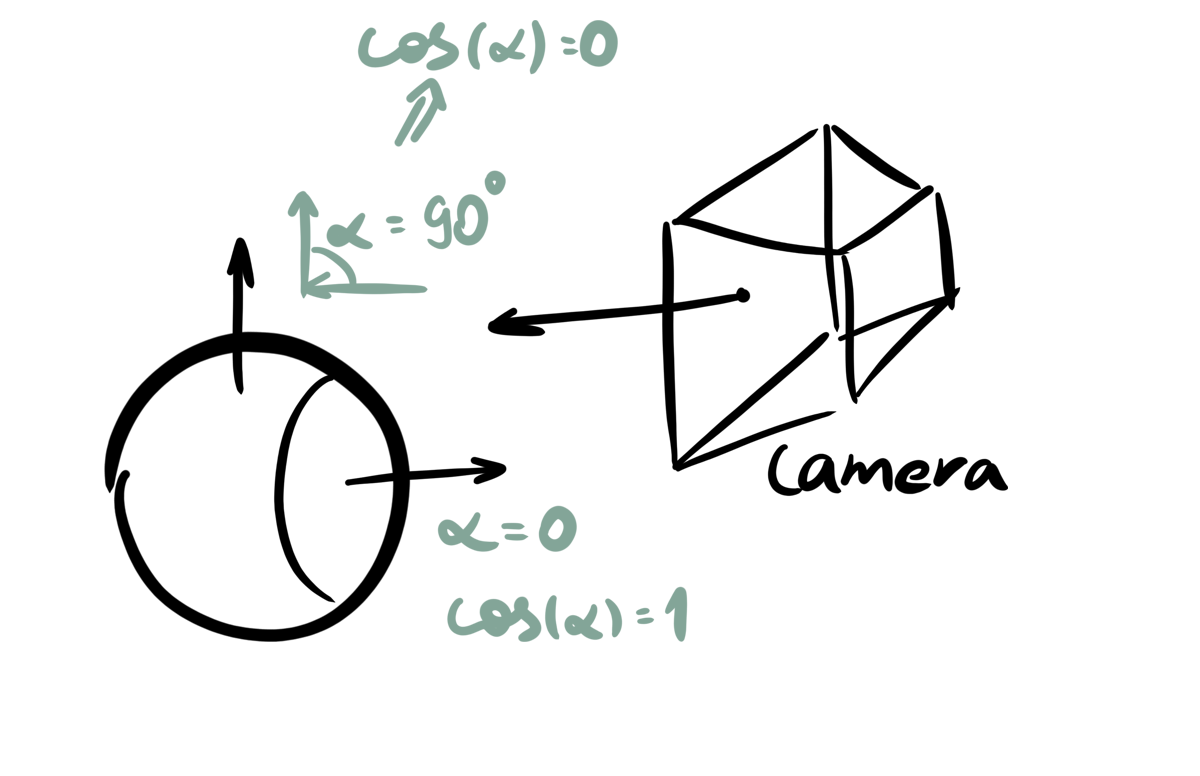
float dist = pow(1.0 - dot(NORMAL, VIEW), power);
// ...

We need to subtract the cosine from 1 in order to get the distance to the edge. We don’t care about vector lengths as in dot product formula \(a \cdot b = \text{len } a \text{ len } b \cos{\theta}\), because NORMAL and VIEW vectors are normalized: their length is 1. Power of value sets the thickness of the edge.

Now, we need to get the color of the dots. I’ve decided to use the position of the fragment from camera to split the model into several zones. As a result, we can determine the CMYK color of each zone.

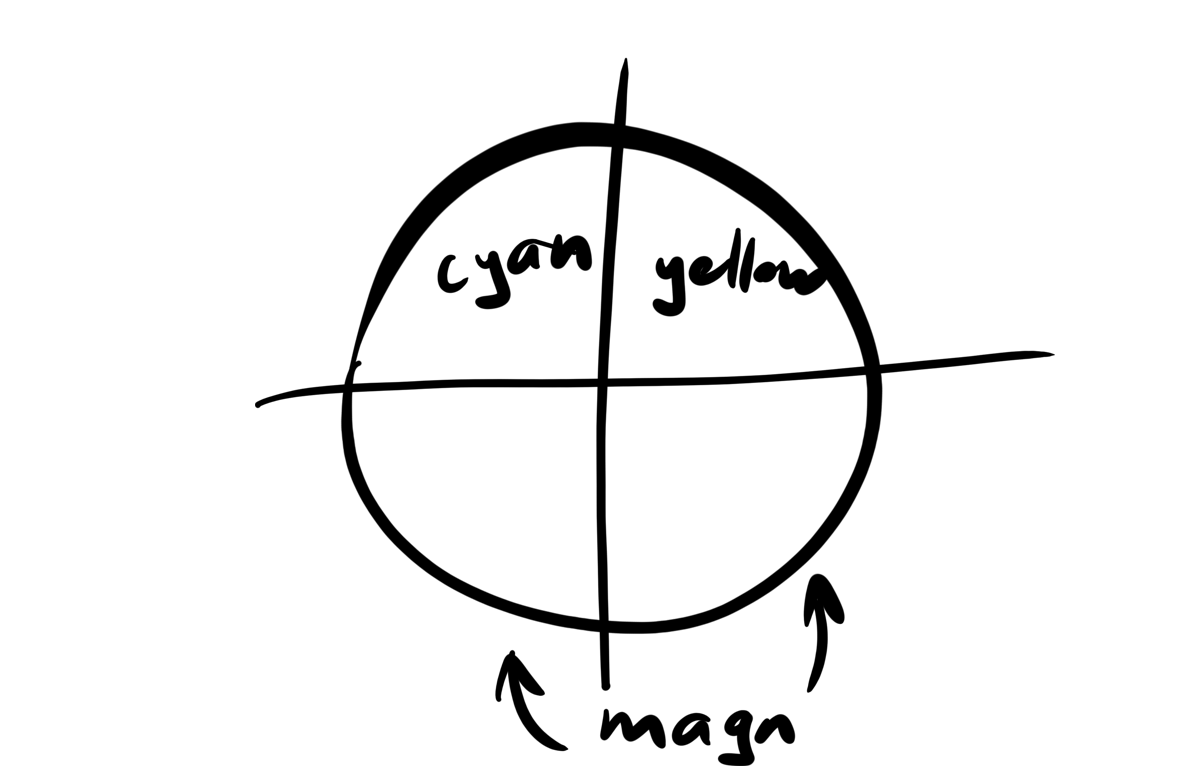
In order to add some variation, we subtract it from the normal. There are better ways to do this, but the current code works fine.

// ...
col = vec3(0.0, 0.0, 0.0);  // set the color to black

if (dist > 0.01)  // check for the edge
{
    col = vec3(0.0, 1.0, 1.0);  // set the color to cyan
    if (NORMAL.x - VIEW.x > 0.0) col = vec3(1.0, 1.0, 0.0);  // yellow
    if (NORMAL.y - VIEW.y < 0.0) col = vec3(1.0, 0.0, 1.0);  // magn
    
    col = dots(SCREEN_UV * VIEWPORT_SIZE, col, vec3(0.0, 0.0, 0.0), 0.0);  // right now we don't set the rotation
}

ALBEDO = col;

SCREEN_UV * VIEWPORT_SIZE returns the position multiplied by the screen size with the respect to the aspect ratio. Perhaps it may be needed to normalize this vector in order to get consistent dot sizes on any screen.

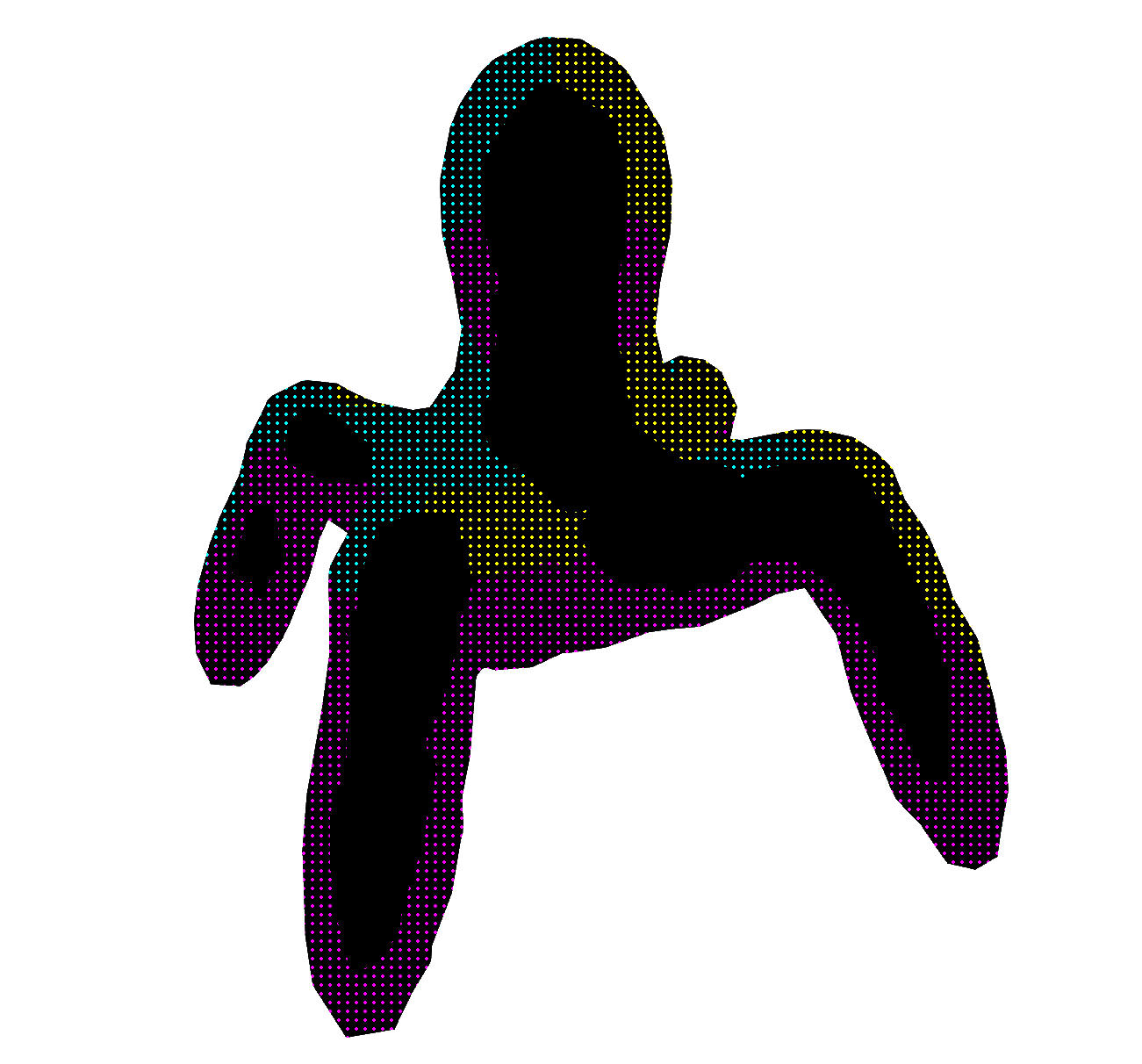
At this step we can see that the model needs some border. We will color it with the corresponding CMYK value. We do it by simply adding another distance check.

// ...
if (dist > 0.01)
{
    col = vec3(0.0, 1.0, 1.0);
    if (NORMAL.x - VIEW.x > 0.0) col = vec3(1.0, 1.0, 0.0);
    if (NORMAL.y - VIEW.y < 0.0) col = vec3(1.0, 0.0, 1.0);
}
if (dist > 0.01 && dist < 0.1)
{
    col = dots(SCREEN_UV * VIEWPORT_SIZE, col, vec3(0.0, 0.0, 0.0), 0.0);
}
// ...

This is much better! Now the model stands out from the rest of the scene. Now we should add the distance check and disable the dots when we are too far away to prevent movement sickness.

// in the uniforms declaration
uniform float dots_hiding_threshold = 0.005;

// ...

void fragment()
{
    vec3 col = vec3(0.0, 0.0, 0.0);
    float dist = pow(1.0 - dot(NORMAL, VIEW), power);
    float cam_dist = pow(length(VERTEX - VIEW), 2) * dots_hiding_threshold;

    if (dist > 0.01)
    {
        col = vec3(0.0, 1.0, 1.0);
        if (NORMAL.x - VIEW.x > 0.0) col = vec3(1.0, 1.0, 0.0);
        if (NORMAL.y - VIEW.y < 0.0) col = vec3(1.0, 0.0, 1.0);
    }
    if (dist > 0.01 && dist < 0.1 - cam_dist)  // we do not draw dots if we are too far away
    {
        col = dots(SCREEN_UV * VIEWPORT_SIZE, col, vec3(0.0, 0.0, 0.0), 0.0);
    }
    ALBEDO = col;
}

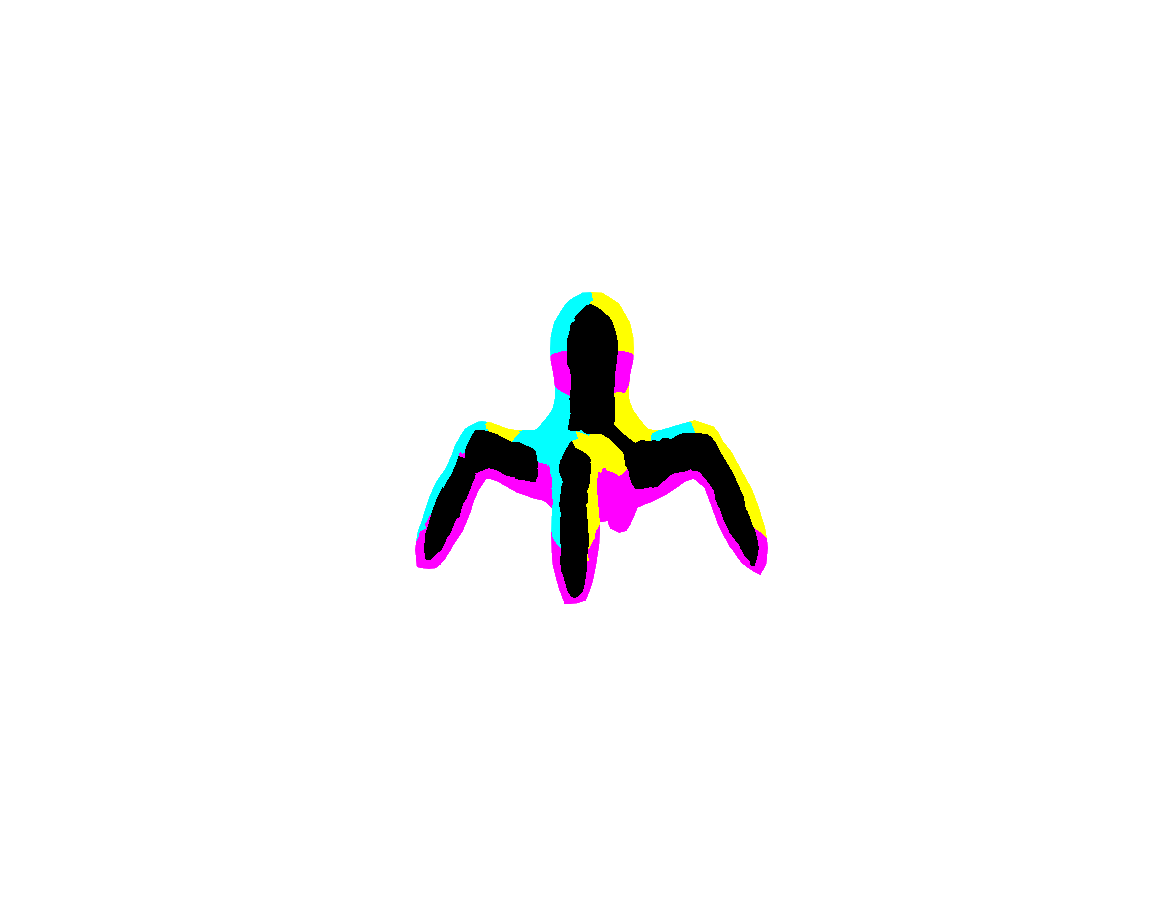
We are too far away and cannot see the dots. The last thing that we would need to implement is the rotation and movement of the dots. We would need some kind of hash function to add random movement. Such function is sine/cosine: if we pass TIME variable, we will get wave-like change of the parameter over time. If we sum two of these functions with different parameters, we would get pseudo random oscillation that repeats over some time. Such functions \(a_1 \sin{(t + b_1)} + ... + a_n \sin{(t + b_n)}\) are called wave functions and are actually used in water shaders. Acerola has a nice video on this topic

I didn’t declare these constants to the uniform variables to avoid the cluttering of the settings window. Feel free to play around with those.

// ...
if (dist > 0.01)
{
    col = vec3(0.0, 1.0, 1.0);
    if (NORMAL.x - VIEW.x*cos(TIME+b_1)*a_1+c_1 > 0.0) col = vec3(1.0, 1.0, 0.0);
    if (NORMAL.y - VIEW.y < 0.05 + sin(TIME+b_2)*a_2+cos(TIME+b_3)*a_3) col = vec3(1.0, 0.0, 1.0);
}
if (dist > 0.01 && dist < 0.1 - cam_dist)
{
    col = dots(SCREEN_UV * VIEWPORT_SIZE, col, vec3(0.0, 0.0, 0.0), a_x*col.x*sin(TIME)/a_s + a_y*col.y + a_z*col.z);
}
// ...

In order to get random rotation for each color, we perform some ‘hash’ formula on the color r, g, b values.

Repository

The code and models are available on Github: https://github.com/enaix/godot-cmyk-dot-shader

Final code version

shader_type spatial;

render_mode unshaded;

uniform float power = 3;

uniform float dot_spacing = 10;
uniform float dot_size = 2;
uniform float dots_hiding_threshold = 0.003;

const float a_1 = 2.0;
const float a_2 = 0.1;
const float a_3 = 0.12;

const float b_1 = 0.0;
const float b_2 = 0.0;
const float b_3 = 2.0;

const float c_1 = -0.3;

const float a_x = 14.3;
const float a_y = 13.2;
const float a_z = 43.3;
const float a_s = 10000.0;

vec3 dots(vec2 pos, vec3 dotcol, vec3 black, float a)
{
    pos = mat2(vec2(cos(a), sin(a)), vec2(-sin(a), cos(a))) * pos;
    if (pow(mod(pos.x, dot_spacing) - dot_size, 2) + pow(mod(pos.y, dot_spacing) - dot_size, 2) <= dot_size*dot_size)
    {
        return dotcol;
    }
    return black;
}

void fragment()
{
    vec3 col = vec3(0.0, 0.0, 0.0);
    float dist = pow(1.0 - dot(NORMAL, VIEW), power);
    float cam_dist = pow(length(VERTEX - VIEW), 2)*dots_hiding_threshold;

    if (dist > 0.01)
    {
        col = vec3(0.0, 1.0, 1.0);
        if (NORMAL.x - VIEW.x*cos(TIME+b_1)*a_1+c_1 > 0.0) col = vec3(1.0, 1.0, 0.0);
        if (NORMAL.y - VIEW.y < 0.05 + sin(TIME+b_2)*a_2+cos(TIME+b_3)*a_3) col = vec3(1.0, 0.0, 1.0);
    }
    if (dist > 0.01 && dist < 0.1 - cam_dist)
    {
        col = dots(SCREEN_UV * VIEWPORT_SIZE, col, vec3(0.0, 0.0, 0.0), a_x*col.x*sin(TIME)/a_s + a_y*col.y + a_z*col.z);
    }
    ALBEDO = col;
}